この記事では、
①MV(Mean Varience)アプローチや初歩的なポートフォリオ理論で使われる意味での「リターンとリスク」の計算
②そこに一定の前提を加えることで導かれる「最適ポートポーフォリオ」
について見ていく。
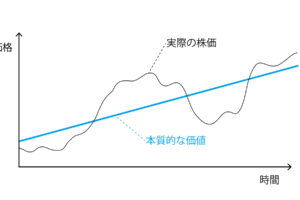
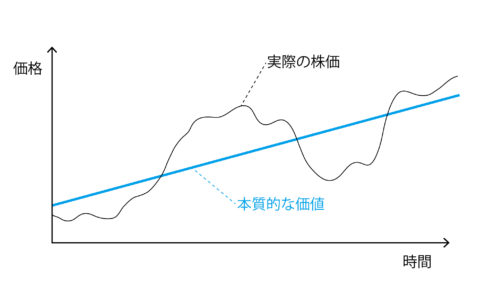
リターンとリスクについての理解は「最適ポートポーフォリオ」の結論
「リスク許容度によって投資対象の中身は基本的に変化しない」
「リスク資産の最適なポートフォリオは1つだけ」
という、大多数の投資家に重要な投資行動の指針を与えてくれる。
つまり、お手軽に無難な投資を行うことを目指せば良い平凡な投資家は「最も超過リターンとリスクの関係が良い(と思われる)リスク資産の最適なポートフォリオ」に投資して―実際には、投資が容易であり最適ポートフォリオに近いと思われる「低コストのインデックスファンド」―を中心に投資して、リスクの調整は現金や国債などの安全資産の比率を増減させるという、シンプルな運用を行えば良いということだ。リスク許容度に応じてリスク資産の中身を選択するなんて余計なことはしなくていい。
例えば、以下のようなアドバイスは一見もっともらしく思えるが、よく考えるどうも怪しいようだ。
「リスク許容度が高いので、新興国株式やオルタナティブ投資の割合を増やそう」
「リスク許容度が低いので、リスク資産の中でも株式の割合を減らしてREITなどを増やそう」
著名なバリュー投資家たちもこう言っている。
「何も知らない投資家 は、例]えば定期的にインデックスファンドに投資すれば、ほとんどのプロの投資家のパフォーマンスを上回ることができます。 」ウォーレン・バフェット
「マーケットを負かすことができないならば自分がマーケットになればよい」セス・クラークマン Margin of Safty
MVアプローチでのリターンとリスクを見ると、「リスク許容度に応じた投資対象を選ぶべき」という考え方はかなり怪しいことになる。金融機関には、貴方から多額の資産を預かろうとするインセンティブがあり、「リスク許容度に応じて望ましいポートフォリオを提供します」というのはそのために非常に都合の良い言葉になる。預金や国債から得られる利益は、他の金融商品に比べれば金融機関に旨味が少ない。しかし、直観的に言っても、株式などリスク資産への投資を縮小することは最も分かりやすく確実なリスク管理の方法である。。
では、まずMVアプローチの意味するMean(平均)とVarience(分散)を順に見ていこう。
目次
1.期待リターン:50%以上達成できない期待リターン
リターンと言えば、ふつう期待リターン、つまり将来起こりそうなリターンの平均値を意味する。
平均値のことを統計学ではMeanと呼び、MVアプローチのMはここから来ている。
ある資産の期待リターンの計算は、次のようになる。
$$期待リターン=\sum_{i=1}^n P_iR_i$$
$$P_i =iの発生する確率 R_i=iの時のリターン$$
期待リターンなどと言っても、半分ぐらいの確率で実現しない―期待リターンを下回ってしまうことに注意して欲しい。例えば、偏りのない模範的なサイコロなら期待値は3.5だが、50%の確率で1,2,3のどれかの出目が出て、期待値である3.5を下回ってしまう。
$$サイコロの期待値=\frac{1}{6}*1+\frac{1}{6}*2+\frac{1}{6}*3+\frac{1}{6}*4+\frac{1}{6}*5+\frac{1}{6}*6=3.5$$
株式投資の収益率は、サイコロのように左右対称で等間隔に並んでいるということはない。有限責任により損失の方には限りがあるのとは対照的に、利益の方に上限はない。実際のところ、収益率の分布は負の歪度を持つ(下図のように左裾が広がった形状になる)可能性が高い。つまり、期待値を下回る確率は半分よりもさらに高そうなのだ。
【負の歪度の分布の図】
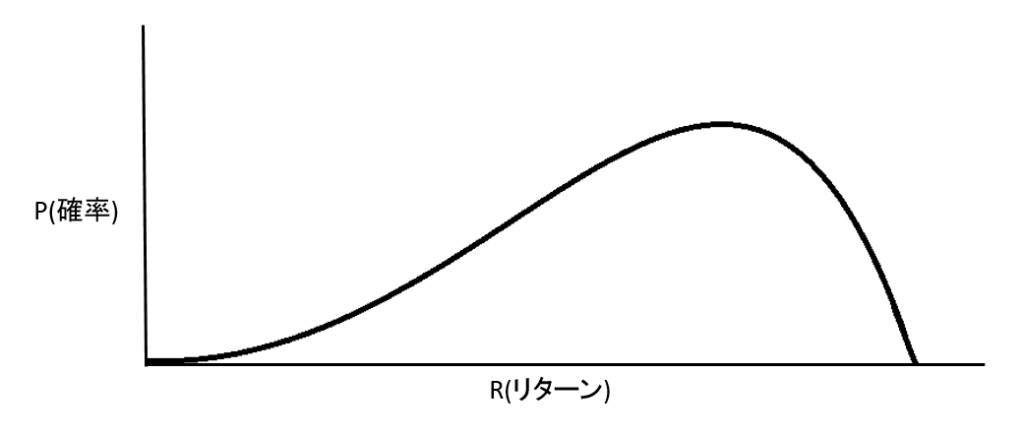
負の歪度
複数の資産をまとめたポートフォリオ全体の期待値はどう計算するのか?
計算は非常に簡単だ。単純に資産の割合ごとに加重平均するだけだ。
$$ポートフォリオの期待リターン=\sum_{i=1}^n W_iE(R_i)$$
$$W_i=資産iの占める割わい E(R_i)=資産iの期待リターン$$
2.数学的に簡単なリスク―ボラティリティ
ボラティリティ(分散)と標準偏差の計算
リスクと言った場合、いろいろものがある。ここでは分散(とその正の平方根である標準偏差)についてみていく。数式の苦手な人には難しく感じるかもしれないが、これでもリスクを数量的に扱う中では簡単な部類(だからそれなりに使われている)ので、少し頑張ってみて欲しい。
分散は、起こり得るかもしれない収益率が期待リターンからどれだけ散らばっているかを示している。分散が大きければ、期待値からより離れた値をとる可能性の高さ、より大きく離れた値を取りうることを示唆している。
リターンに関する分散の計算は次のようになっている・
$$V(R)=E((R-E(R))^2)$$
言葉にすると「偏差(予想される収益率と期待リターンとの差)の二乗の期待値」となる。偏差の絶対値の期待値ではなく、偏差の二乗の期待値を取るのは数学的に扱いやすいからであるようだ。
分散の正の平方根のことを標準偏差と言い、リスク(%)などと表記される時はだいたいこの意味で使われσ(ギリシア文字で「シグマ」と読む)と表記される。
$$分散=σ^2$$
$$標準偏差=σ=\sqrt(σ^2)$$
ポートフォリオのボラティリティ
2資産の組み合わせの分散は次のように計算できる。
$$σ^2=W_x^2σ_x^2+W_y^2*σ_y^2+2W_xW_yCov_{xy}$$
$$=W_x^2σ_x^2+W_y^2*σ_y^2+2W_xW_yσ_xσ_yρ_{xy}$$
$$Cov_{xy}:資産x,yの共分散(covarience)=E【{X-E(X)}{Y-E(Y)}】=ρσ_xσ_y$$
・共分散は「偏差の積」の平均で以下のような性質がある。
・正の値で大きい→XとYの連動性が強い(Xが高いとYも高い傾向)
・0に近い→XとYはあまり関係がない。
・負の値で大きい→XとYは逆に連動する(Xが高いとYは低い傾向)
・XとYの絶対的な大きさの影響を受ける。
・相関係数$$σ(=Cov_{xy}/σ_xσ_y)$$は1が最大、-1が最低で規格されたもの。
ポートフォリオの分散は、
・各資産の分散
・各資産間の相関(共分散・相関係数)
・各資産への投資割合
で決まり、特に各資産間の相関が大きな影響を与える。相関系数が小さければポートフォリオの分散は加重平均よりも小さくなり、分散投資のメリットを享受できる。逆に相関係数が大きければ分散のメリットはほとんど得ることができない。
3.望ましいポートフォリオはたった1つか?マーケットポートフォリオと資本市場線
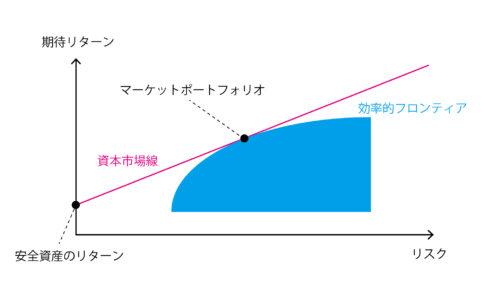
株式などいくつかのリスク資産の組み合わせを考えていくと、投資可能な領域ーつまり、リスクに対して取りうる期待リターンの図(下図の青色の部分)を描くことができる。投資可能な領域の中で所与のリスクに対して最大のリターンをもたらす上の境界線の部分を効率的フロンティアと呼ぶ(正確には「リスク資産の効率的フロンティア」)。MVアプローチによれば、所与のリスクに対して最大の期待リターンが得られる場所、つまり効率的フロンティアの中から投資対象を選ぶべきということになる。
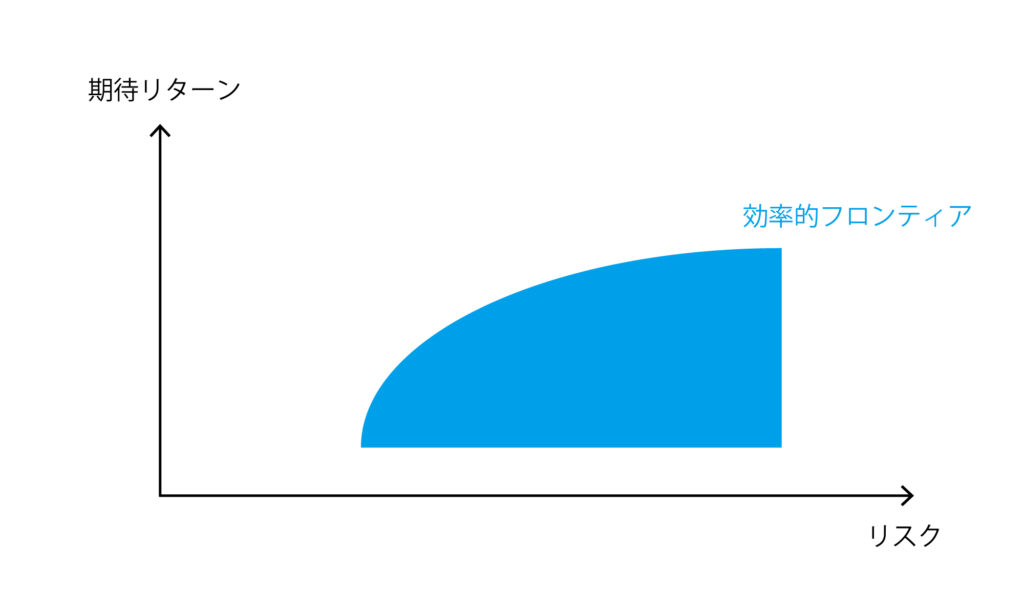
効率的フロンティア
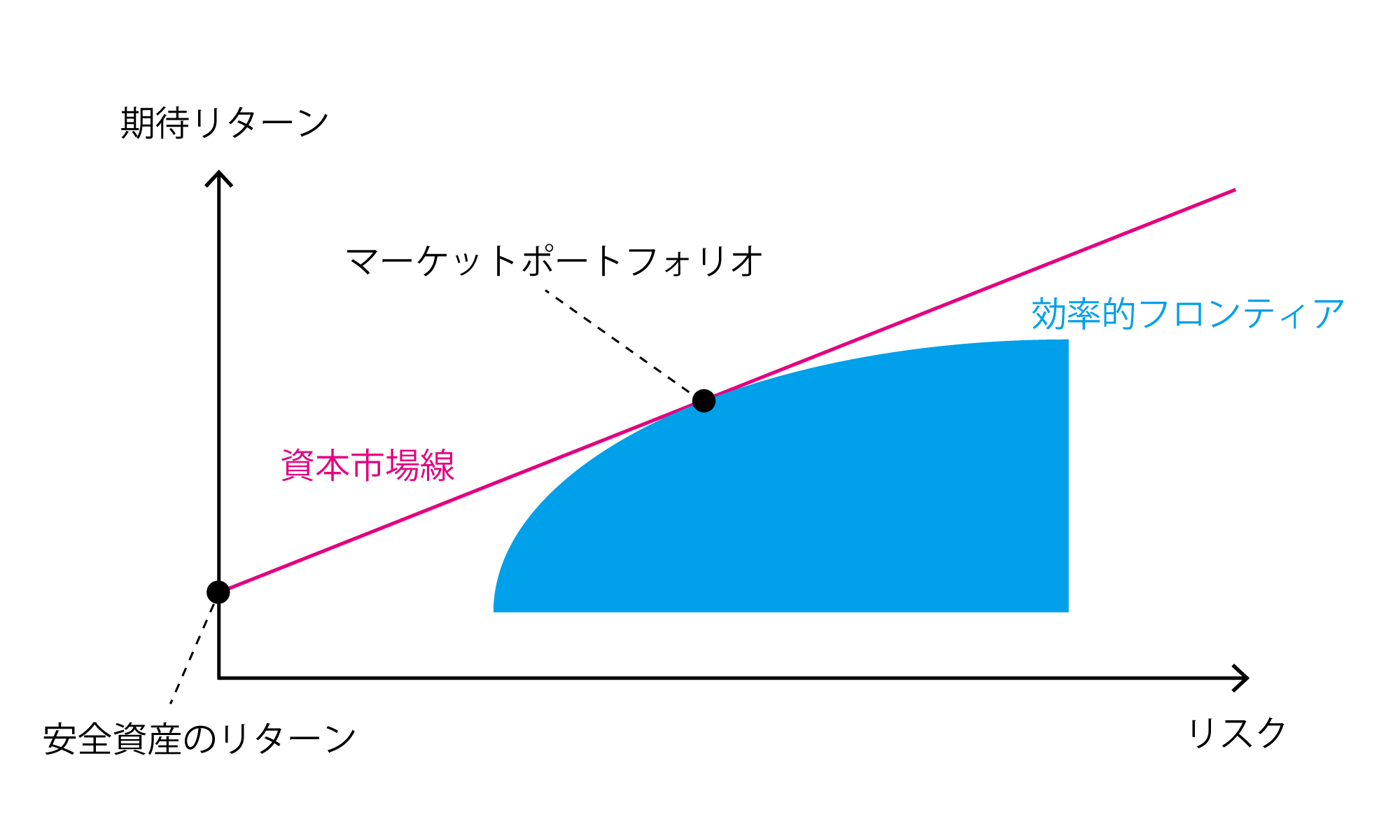
完全な市場を仮定して、さらに無リスク資産(安全資産)への投資と借入まで考慮すると、投資家が選ぶべきリスク資産の内容はたった1つに決まる。
この点が示す「リスク資産のポートフォリオ」は「市場ポートフォリオ」または「マーケット・ポートフォリオ」と呼ばれるもので、全ての投資家における、リスク資産の最適なポートフォリオを示している。
投資家は、自分のリスク許容度に応じて、この「市場ポートフォリオ」と「安全資産(+借入)」との比率を調整すればよい(下図の「資本市場線」からリスク許容度に合った点を安全資産を増減させることで選べばよい)。
※「安全資産」と「リスク資産」の相関は0と仮定され、安全資産とマーケットポートフォリオによる投資可能な領域は、両者を結ぶ直線で表すことができる。さらに借入まで考慮すると、マーケットポートフォリオからさらに延長して線を描くことができる。下図で明らかなように、資本市場線は、接点を除いて、リスク資産の効率的フロンティアを上回っている。
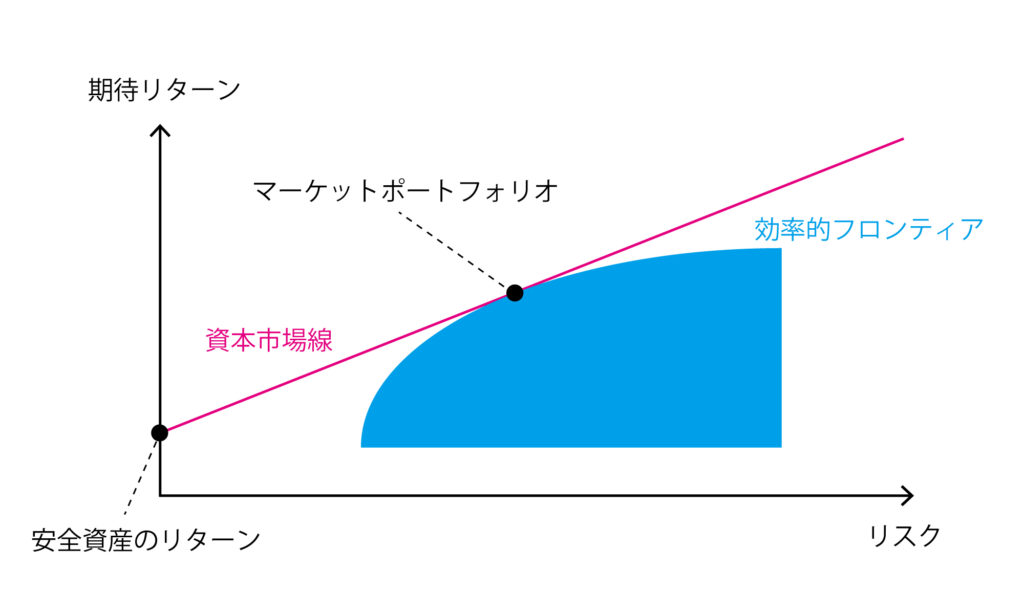
資本市場線(CML:Capital market line)
前提条件に非現実的なところはあるが、
最適なリスク資産の中身は、平凡な投資家にとってほとんど変わりがない
リスク管理は投資額の増減でも行えるし、その方が有利な場合も多い
という点は是非とも覚えておいて欲しい。
MVアプローチは、投資の基準を期待リターンとは分散(ボラティリティ)のみで考えている。
そこには、リスクの測定は分散で十分という前提あるいは、より複雑なリスクの測定は扱いや顧客の理解が困難ということがあるのかもしれない。他にリスクを表す可能性があるものとして、例えば、VaR(Value at Risk)や分布の尖度や歪度などがある。
分散がリスクの全てではないが、個人投資家はそれほど複雑なものに立ち入らなくてもいいだろう。
4.低コストでインデックス投資―コストの高い「ラップ口座」には注意
最適なリスク資産の中身は、普通の投資家にとってほとんど変わりがない―インデックスファンド―のであれば、取り組むべきはいかにコストを抑えるかだ。
「投資はマーケットと比較すればゼロサムゲームなのである。」ブルース・グリーンウォルド
株式投資から得られる投資家全体の利益は、株式会社が稼ぐCFから最初の出資額を引いたものだ。優秀なファンドマネージャーが、投資家全体の利益を増やすことは直接的にはありえない。また、コストを払ってでもマーケットを上回る優秀なファンドマネージャーはほとんど存在しない、あるいは存在するとしても事前に見分けることが難しい、アクセスすることは難しいとする意見も根強い。
だから、超過リターンを得ることができないと考えられる―普通の平凡な投資家は、低コストのインデックスファンドに(なるべく自分で)投資しよう。そうすれば余計な手数料をとられなくて済む。
「バランス・ファンド」は、お手軽に無難な投資を行うにはいいかもしれないが、自分でインデックスファンドを組み合わせて同等のものを作ってしまった方が安上がり(リスクを減らしたい場合は、投資額を減らすことでも解決できる)な場合もあるので、コストには注意しておこう。
同様の理由で「ラップ口座」はバランスファンド以上にオススメできない。ラップ口座自体に信託報酬を支払い、さらにラップ口座内で投資する高コストのファンドのコストも負担するシステムになっていることが多いからだ。酷いものでは、年間の資産3%程度のコストを負担しているものもあった。
株式投資の超過リターンは歴史的には年間5~8%程度なのに、金融機関に毎年資産額の1~3%も払うのはバカバカしいと言うほかない(株式より期待リターンの低い金融資産が含まれるなら尚更だ)。
まとめ
・期待リターンは少なくとも半分程度の確率で達成できない。分散はリターンのバラツキの程度を示す。
・複数の資産のリターンは個々の資産のリターンと投資割合で決まり、分散は個々の資産の分散と相関と投資割合で決まる。
・投資額の縮小は最も分かりやすく確実なリスク管理。
・平凡な投資家にとって望ましいリスク資産の内容は大きく変わらないし、インデックスファンドで誰でも比較的容易に無難な投資ができる。
・低コストなETFを自分で組み合わせるのが望ましい。どうしても面倒を避けたいならバランスファンドやネット証券系のラップ口座などからなるべく低コストなものを選ぼう。










はじめまして。現在、証券会社で営業しています。ラップ口座は、お客さまにも人気で、営業としてはありがたい商品です。確かにラップ口座の手数料は高めですが、それは、証券会社がお客さまをサポートする費用として頂戴しているので、1〜3%の手数料は妥当です。と言いたいところですが、読んでみると、確かにおっしゃる通りですね。ラップ口座を提案しづらくなりました。